This post explains the paper “CLOOB: Modern Hopfield Networks with InfoLOOB Outperform CLIP”.
CLOOB (Contrastive Leave One Out Boost) is a novel self-supervised learning method, where modern Hopfield networks boost contrastive learning using the InfoLOOB objective (Leave One Out Bound). CLOOB consistently outperforms CLIP at zero-shot transfer learning across different architectures and datasets.
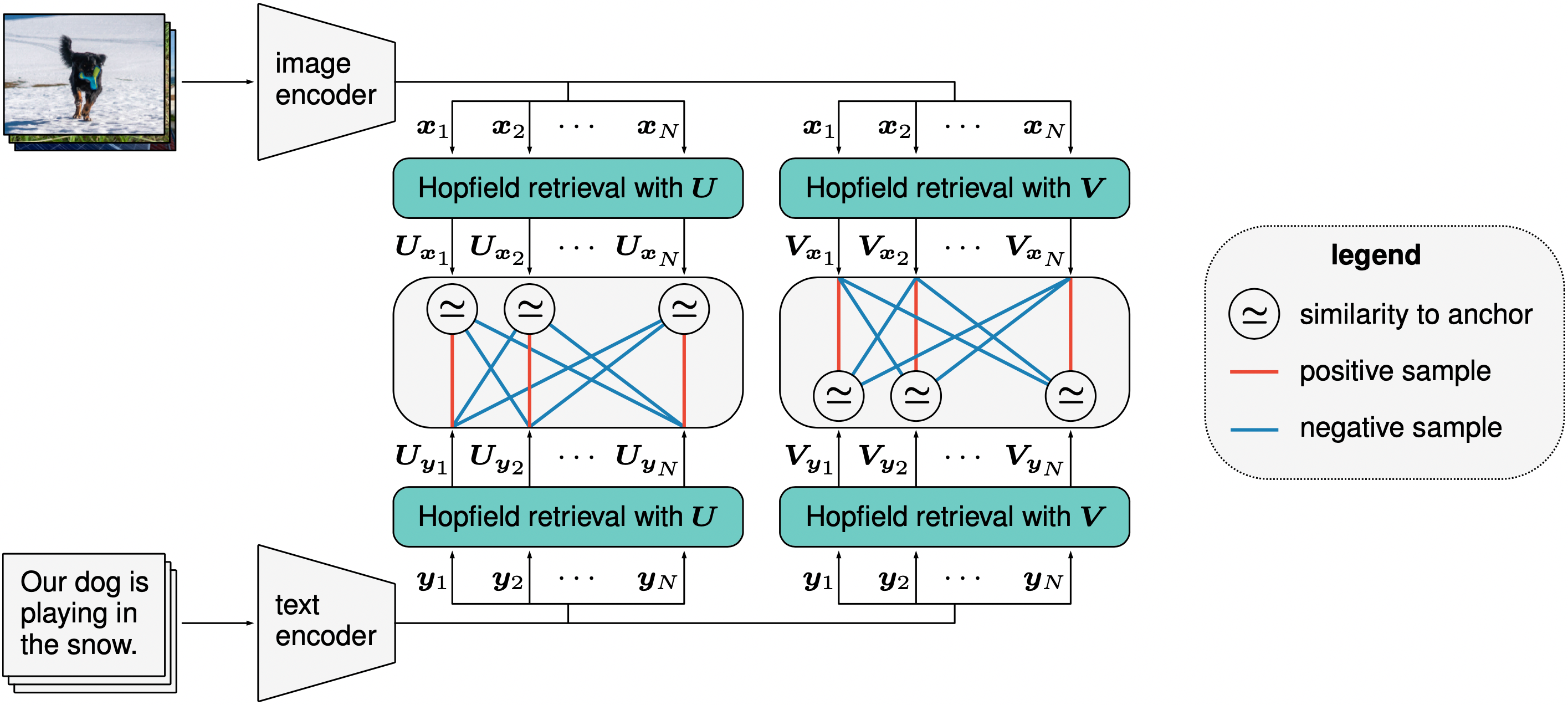
A sketch of CLOOB and zero-shot transfer learning results for CLOOB and CLIP (YFCC pretraining):
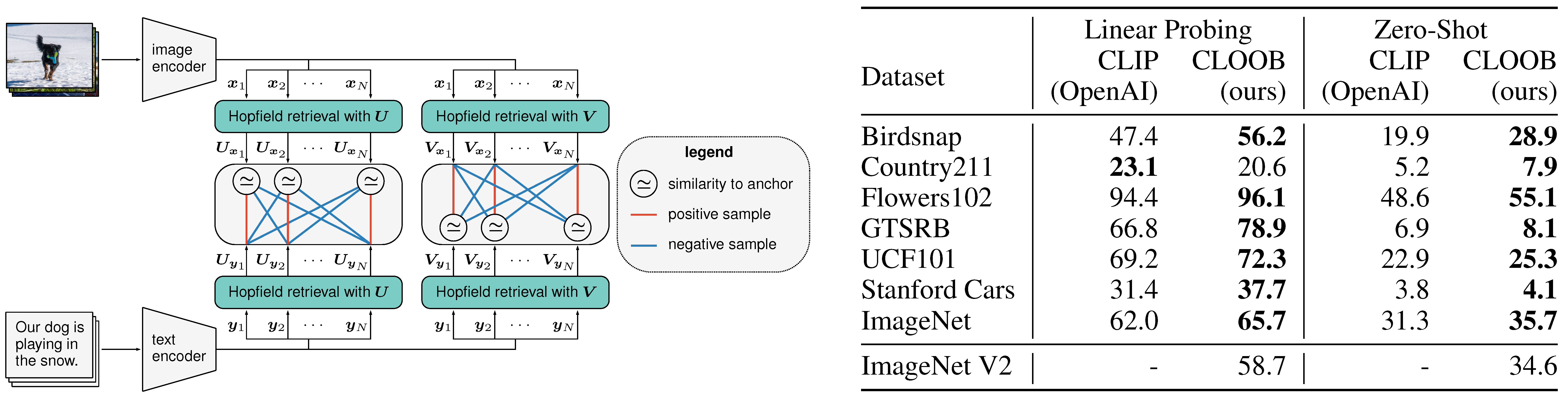
Table of Contents
- CLOOB: Modern Hopfield Networks with InfoLOOB
- Introducing CLOOB to Solve the Explaining Away Problem of CLIP
- Modern Hopfield Networks to Tackle the Explaining Away Problem
- InfoLOOB to Avoid InfoNCE’s Saturation Problem
- Experiments
- Code and Paper
- Additional Material
- Correspondence
CLOOB: Modern Hopfield Networks with InfoLOOB
We introduce CLOOB (Contrastive Leave One Out Boost), a novel contrastive learning method that overcomes problems of the recently introduced CLIP (Contrastive Language-Image Pre-training)(Radford et al., 2021). Contrastive learning has two simultaneous goals:
-
Increasing the alignment (similarity of matched pairs).
-
Increasing the uniformity (dis-similarity of unmatched pairs).
Compared to CLIP, CLOOB increases the uniformity while preserving the alignment by introducing two new components:
-
CLOOB utilizes modern Hopfield networks to extract more covariance structure during learning. CLOOB substitutes the embeddings of the input sample by embeddings that are retrieved from a modern Hopfield network storing reference samples. Therefore CLOOB solves CLIP’s problem of insufficiently extracting feature co-occurences and covariance structure in the original multi-modal data.
-
CLOOB uses InfoLOOB as objective to avoid the saturation of the InfoNCE objective used in CLIP. Modern Hopfield networks exacerbate the saturation problem of the InfoNCE objective caused by the increased similarity of retrieved samples. InfoLOOB does not suffer from saturation.
CLOOB Architecture
A sketch of CLOOB. In this example, we sample text-image pairs where each text describes the corresponding image.
The \(i\)-th input image is mapped by an image encoder to \(\Bx_i\) living in an embedding space. Analogously, the \(i\)-th input text is mapped by a text encoder to \(\By_i\) living in the same embedding space. The \((\Bx_i, \By_i)\) are anchor-positive pairs, where each of the two components can serve as an anchor.
The image embedding \({\Bx}_i\) and the text embedding \(\By_i\) retrieve the embeddings \(\BU_{\Bx_i}\) and \(\BU_{\By_i}\), respectively, from a modern Hopfield network that stores image embeddings \(\BU\) (two green boxes in the left block). The retrieved image embedding \(\BU_{\Bx_i}\) serves as anchor in order to contrast the positive image embedding \(\BU_{\By_i}\) with the negative image embeddings \(\BU_{\By_j}\) for \(j \ne i\). Analogously – for the second modern Hopfield network that stores text embeddings \(\BV\) (two green boxes in the right block).
In the following the CLOOB objective, which is the sum of InfoLOOB with \(\BU_{\Bx_i}\) as anchor (positive: \(\BU_{\By_i}\); negatives: \(\BU_{\By_j}\)) and InfoLOOB with \(\BV_{\By_i}\) as anchor (positive: \(\BV_{\Bx_i}\); negatives: \(\BV_{\Bx_j}\)), is shown:
\[\begin{align} \label{eq:cloob} \rL_{\mathrm{InfoLOOB}} &= - \frac{1}{N} \ \sum_{i=1}^N \ln \frac{\exp (\tau^{-1} \ \BU_{\Bx_i}^T \BU_{\By_i})} {\sum_{j \ne i}^N \exp (\tau^{-1} \BU_{\Bx_i}^T \BU_{\By_j})} - \frac{1}{N} \sum_{i=1}^N \ln \frac{\exp (\tau^{-1} \ \BV_{\Bx_i}^T \BV_{\By_i})} {\sum_{j \ne i}^N \exp (\tau^{-1} \ \BV_{\Bx_j}^T \BV_{\By_i})} , \tag{1} \end{align}\]where the following vectors are retrieved from modern Hopfield networks
\[\begin{align} \BU_{\Bx_i} \ &= \ \BU \ \soft(\beta \ \BU^T \Bx_i ) \ , \quad \BU_{\By_i} \ = \ \BU \ \soft(\beta \ \BU^T \By_i ) \ , \label{eq:u_retrieval} \tag{2} \\ \BV_{\Bx_i} \ &= \ \BV \ \soft(\beta \ \BV^T \Bx_i)\ , \quad \BV_{\By_i} \ = \ \BV \ \soft(\beta \ \BV^T \By_i )\ . \label{eq:v_retrieval} \tag{3} \end{align}\]Introducing CLOOB to Solve the Explaining Away Problem of CLIP
Self-supervised learning based on contrastive objective functions has become highly successful. An unimodal contrastive objective for pretraining of vision models contrasts views of images with views of other images. A multimodal objective would for a given image contrast the corresponding caption to captions of other images or, the other way around, for a given caption contrast the corresponding image to images of other captions.
CLIP, a recent multimodal approach,
yielded very impressive results at
zero-shot transfer learning (Radford et al., 2021).
CLIP learns expressive image embeddings directly from associated language
(image - caption pairs).
These rich embeddings empower CLIP
to become
one of the most important foundation models (Bommasani et al., 2021).
Though CLIP yielded striking zero-shot transfer learning results, it still suffers from “explaining away”. Explaining away is known in reasoning as the concept that the confirmation of one cause of an observed event dismisses alternative causes (Pearl, 1988; Wellman and Henrion, 1993). CLIP’s explaining away problem is its focus on one or few features while neglecting other relevant features. This problem is caused by insufficiently extracting feature co-occurrences and covariance structures in the original multi-modal data.
Humans extract co-occurrences and covariances by associating current perceptions with memories (Bonner and Epstein, 2021; Potter, 2012). For example, objects like a cake can be recognized even if blurred when a teacup is close to it. Humans associate drinking tea with cake because of their past experiences stored in long term memory.

In the following image, the part of the picture above the bed suggests that it is an aquarium. Yet the co-occurence and placement of the pillows, the bed linen and the bedside lamps together strongly suggest a bedroom to humans.

In analogy to these human cognitive processes, we suggest to use modern Hopfield networks to amplify co-occurrences and covariance structures of the original data.
Modern Hopfield Networks to Tackle the Explaining Away Problem
Modern Hopfield Networks. Modern Hopfield networks are associative memories that have much higher storage capacity than classical Hopfield networks and they can retrieve patterns with one update only (Ramsauer et al., 2021; Widrich et al., 2020).
Details about modern Hopfield networks are available in the blog Hopfield Networks is All You Need.
Associative Memory. Similar to the associative memory of humans, our approach uses associative memories to amplify co-occurences and the covariance structure. The associative memory of our choice is a modern Hopfield network because of its fast retrieval and high storage capacity, as shown in Hopfield networks is all you need. The update mechanism of modern Hopfield networks is equivalent to the self-attention mechanism of Transformer networks. However, modern Hopfield networks are more general and have a broader functionality, of which the Transformer self-attention is just one example. The according Hopfield layers can be built in Deep Learning architectures for associating two sets, encoder-decoder attention, multiple instance learning, or averaging and pooling operations. For details, see our blog Hopfield Networks is All You Need.
Amplifying Co-occurences and Covariance Structures to Mitigate Explaining Away. Instead of using directly the embeddings of the input samples, we suggest to use embeddings that are retrieved from a modern Hopfield network that stores reference embeddings. The retrieved embeddings possess richer co-occurrences and covariance structures as they are obtained by averaging over all stored reference samples that are similar to the input sample. Replacing the original embeddings by retrieved embeddings reinforces co-occurences that also appear in reference samples similar to the input sample. Additionally, spurious co-occurences that are peculiar to the input sample are averaged out.
Demonstration of the Advantages of Modern Hopfield Networks. In the following we demonstrate the advantages of using modern Hopfield networks.
- They amplify co-occurences and covariance structures of features that encode the input sample.
- They remove spurious co-occurences that are peculiar to the input sample.
The presence of an object in the input is represented by the activation of certain features. For visualization purpose only, these activated features are arranged as a sketch of this object. For example the features that represent a tea cup are arranged to sketch a tea cup.
In our demonstration the task is to determine the type of location. For example we consider the location of a tea house. This location is characterized by the Tea House Concept consisting of objects which often occur together, like tea pot, tea cup, cake, and fork.
Images from left to right represent:
- The input in a tea house, which indicates objects observed in this location (superimposed).
- The features that are retrieved from the modern Hopfield network by the left image.
- The Tea House Concept.
In the memory of the modern Hopfield networks, input representations of different locations are stored including those of tea houses. Via the retrieval the Tea House Concept is amplified while features peculiar to this input are averaged out.

The following image shows the same for another tea house.
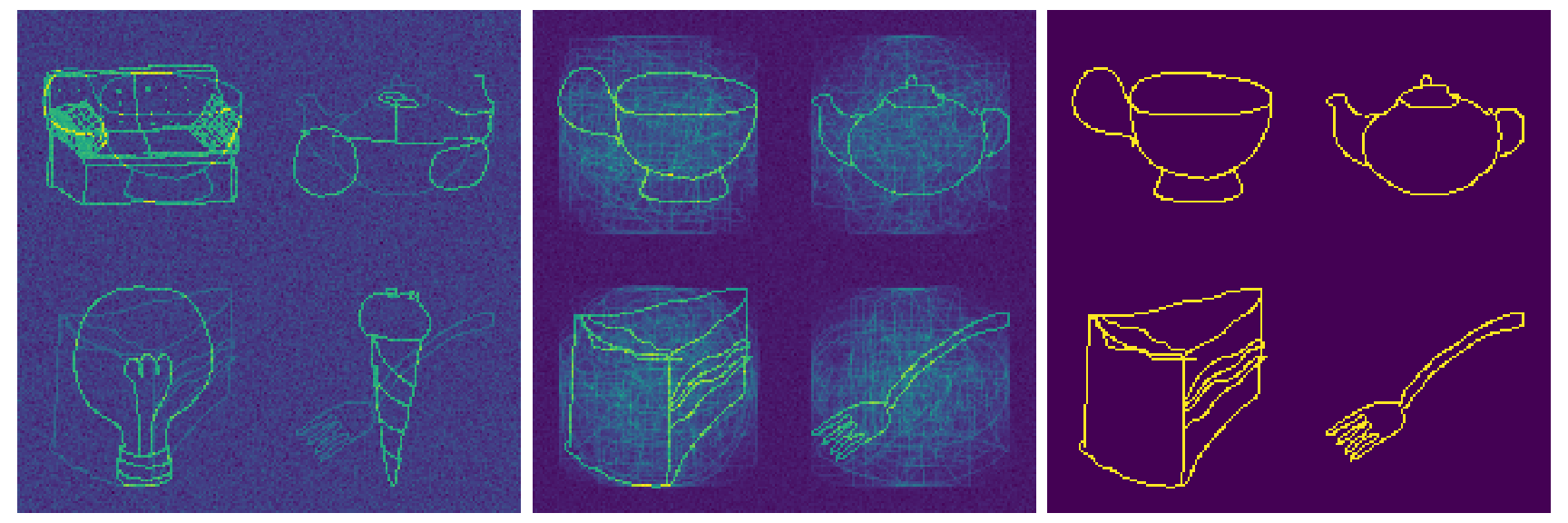
The similarity between the two tea houses is enhanced in the retrieved features (middle image) compared to the features representing the input (left image). The similarity originates from the extracted co-occurence and covariance structure in the retrieved features. Concluding, modern Hopfield networks enhance the co-occurence and covariance structure in the retrieved features.
Modern Hopfield Networks Steadily Extract More Covariance Structure. To demonstrate the effect of modern Hopfield networks, we computed the eigenvalues of the covariance matrix of the image and text embeddings. These embeddings are obtained at two different training points of the image and text encoder. We counted the number of effective eigenvalues, that is, the number of eigenvalues needed to obtain 99% of the total sum of eigenvalues. The following figure shows the relative change of the number of effective eigenvalues compared to the respective reference epoch.
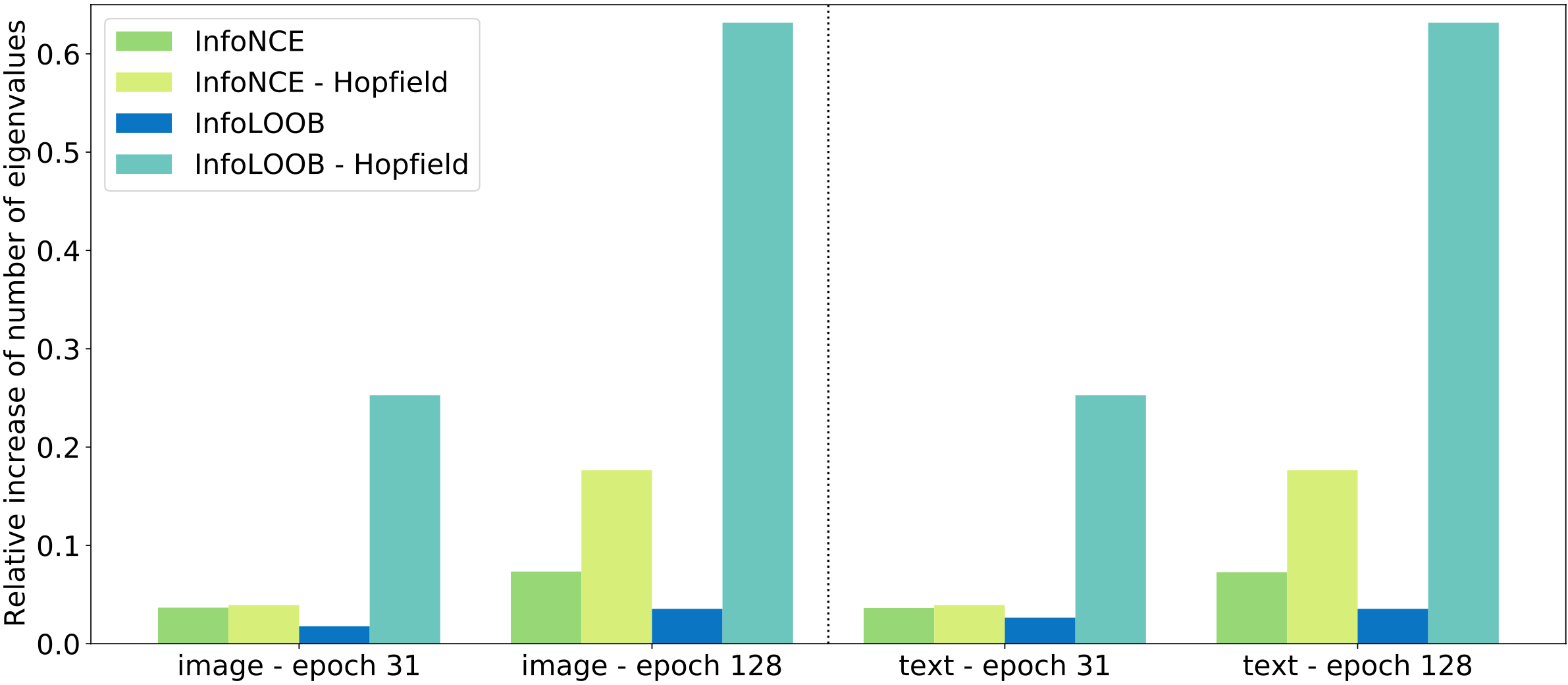
Modern Hopfield networks consistently increase the number of effective eigenvalues during learning. Consequently, modern Hopfield networks enable to extract more covariance structure during learning, thereby mitigate explaining away.
InfoLOOB to Avoid InfoNCE’s Saturation Problem
However, modern Hopfield networks lead to a higher similarity of retrieved samples. The increased similarity exacerbates the saturation of the InfoNCE objective. We propose InfoLOOB as an objective to avoid saturation as observed with InfoNCE.
In the following we formally present the setting and the InfoNCE and InfoLOOB objectives.
The training set consists of \(N\) matched pairs \(\{(\Bx_1,\By_1),(\Bx_2,\By_2),\ldots,(\Bx_N,\By_N)\}\).
In the following objectives, for an anchor sample \(\Bx_i\)
a positive sample \(\By_i\) is contrasted with
negative samples \(\By_j\) (first term of the objective).
Analogously for an anchor sample \(\By_i\)
a positive sample \(\Bx_i\) is contrasted with
negative samples \(\Bx_j\) (second term of the objective).
We get the following InfoNCE and InfoLOOB objectives:
In expectation, \(\exp (\tau^{-1} \ \Bx_i^T \By_i)\) has a high value for a matched pair
and \(\exp (\tau^{-1} \ \Bx_j^T \By_i)\) as well as \(\exp (\tau^{-1} \ \Bx_i^T \By_j)\) have a low value for unmatched pairs.
Saturation of InfoNCE. InfoNCE saturates because it contains terms of the form \(a/(a + b)\). In analogy to Wang and Isola (2020), \(a\) is called the “alignment score” that measures the similarity of matched pairs and \(b\) the “uniformity penalty” that measures the similarity of unmatched pairs.
To exemplify the saturation problem of InfoNCE, we consider the first term in the second sum of the losses from Eq. \eqref{eq:InfoNCE} and Eq. \eqref{eq:InfoLOOB}:
\[\begin{align} \label{eq:InfoNCE_single_term} \rL_{\mathrm{InfoNCE}}(\By) \ = \ &- \ \ln \frac{\overbrace{\exp (\tau^{-1} \ \Bx_1^T \By)}^{a}} {\underbrace{\exp (\tau^{-1} \ \Bx_1^T \By)}_{a} \ {+} \ \underbrace{\textstyle{\sum_{j=2}^N} \exp (\tau^{-1} \ \Bx_j^T \By)}_{b}} \ , \tag{6} \\ \label{eq:InfoLOOB_single_term} \rL_{\mathrm{InfoLOOB}}(\By) \ = \ &- \ \ln \frac{\overbrace{\exp (\tau^{-1} \ \Bx_1^T \By)}^{a}} {\underbrace{\textstyle{\sum_{j=2}^N} \exp (\tau^{-1} \ \Bx_j^T \By)}_{b}} \ . \tag{7} \end{align}\]Obviously, for a large similarity \(a\), the InfoNCE objective saturates and increasing \(a\) has a small effect. The saturation problem becomes more severe for the retrieved samples of a modern Hopfield network since the alignment score \(a\) increases.
InfoLOOB Prevents Saturation. The state where learning is stalled can be avoided by objectives of the form \(a/b\). Such an objective was introduced in Poole et al. (2019), derived from a variational upper bound on the mutual information called “Leave one out upper bound”. In Cheng et al. (2020) this bound is called “L1Out”. For simplicity, we call this bound “InfoLOOB”, where LOOB is an acronym for “Leave One Out Bound”, where the objective is the negative of the bound. The InfoLOOB objective is similar to the InfoNCE objective except that the denominator does not contain a positive sample.
InfoLOOB Leads to More Uniform Representations. InfoLOOB does not saturate and keeps decreasing the uniformity penalty \(b\). The following figure shows how InfoLOOB leads to an increase in the uniformity of image and text embeddings on the sphere, which is described by the statistics of the uniformity test of Ajne extended by Prentice (Ajne, 1968; Prentice, 1978).
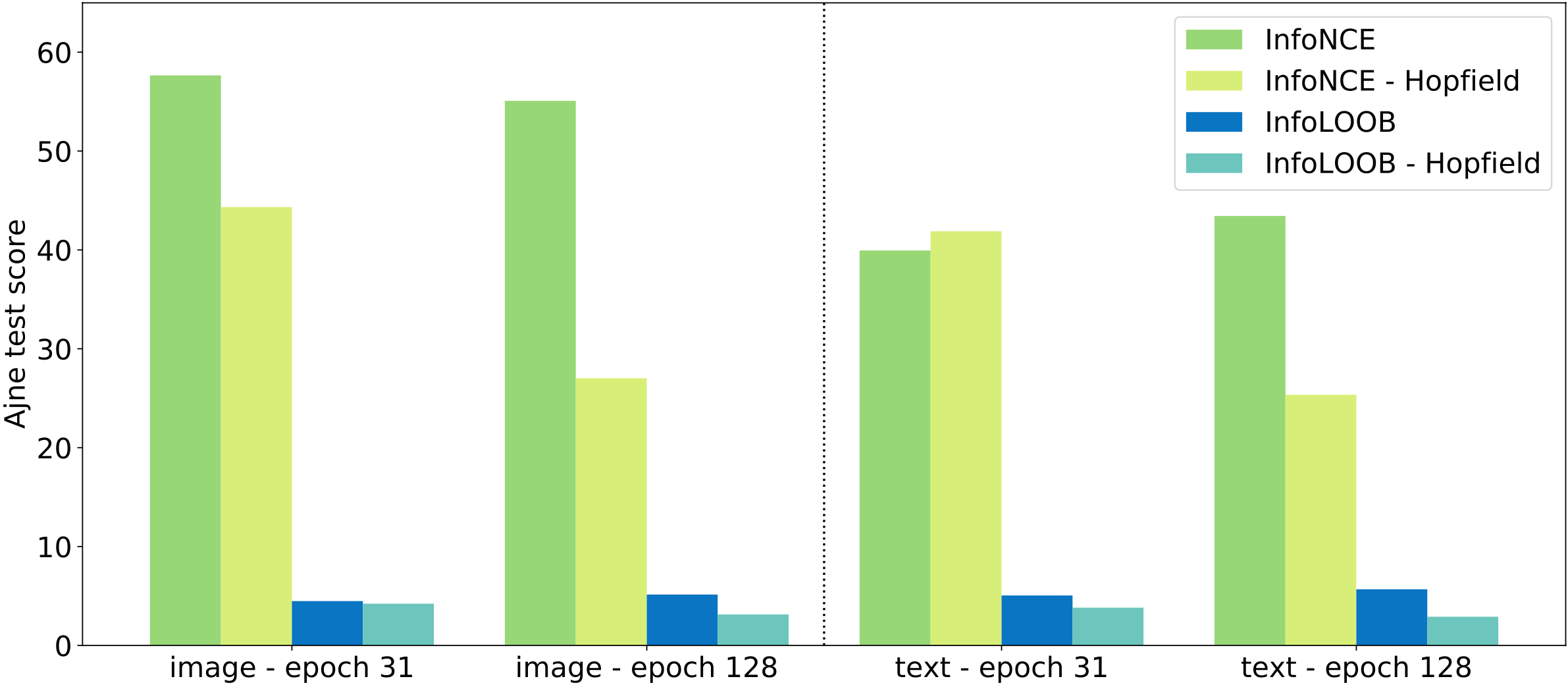
A high Ajne test score indicates low uniformity of an embedding. Models trained with the InfoLOOB objective develop more uniform image and text embeddings on the hypersphere.
Experiments
Methods Compared. The methods CLIP and our new CLOOB are compared (Radford et al., 2021). We use a reimplementation of CLIP from OpenCLIP (Ilharco et al., 2021) to obtain results where results of the OpenAI CLIP were not available.
Evaluation. After pretraining, we evaluate the performance of the methods on seven downstream zero-shot transfer learning tasks with respect to their accuracy.
Conceptual Captions Pretraining
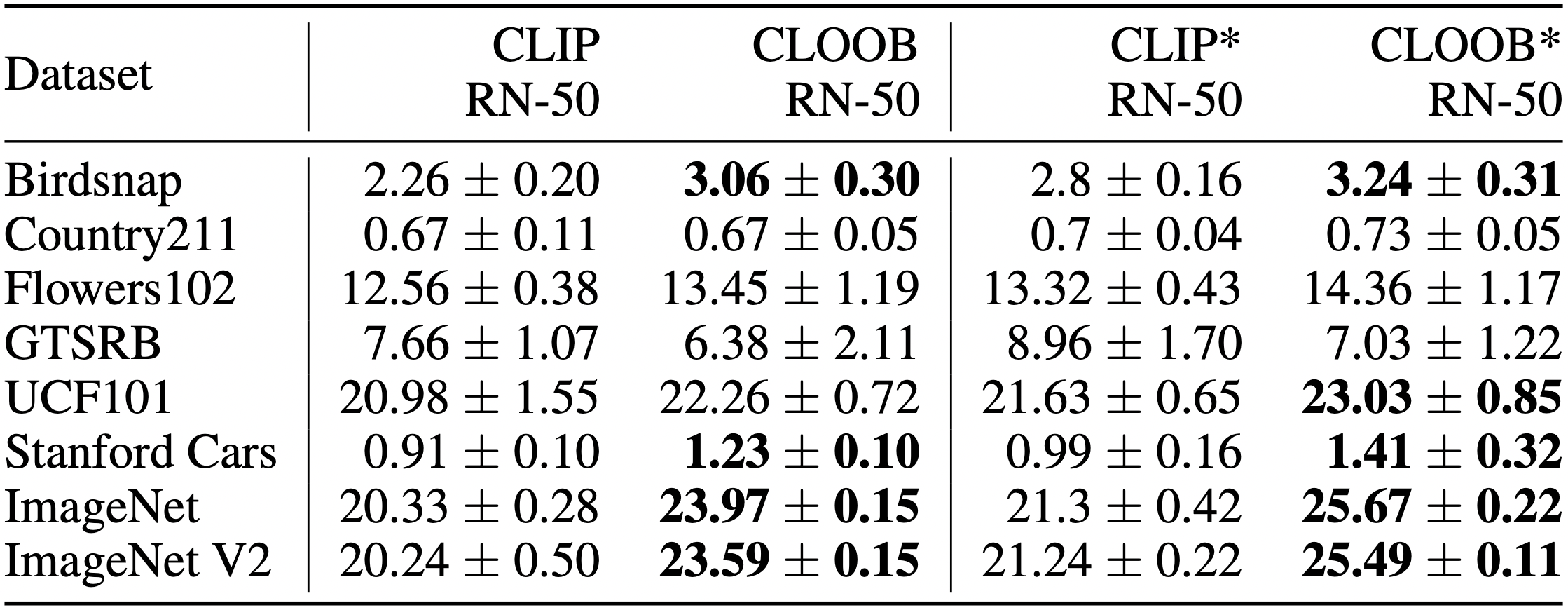
Pretraining Dataset. The Conceptual Captions (CC) (Sharma et al., 2018) dataset has a very rich textual description of images but only three million image-text pairs.
Results. Zero-shot results for models trained on CC with ResNet-50 vision encoders for two different checkpoints. Results show the mean accuracy over 5 runs. Statistically significant results are shown in bold. CLIP and CLOOB were trained for 31 epochs while CLIP* and CLOOB* were trained for 128 epochs. In the majority of tasks CLOOB significantly outperforms CLIP.
YFCC Pretraining
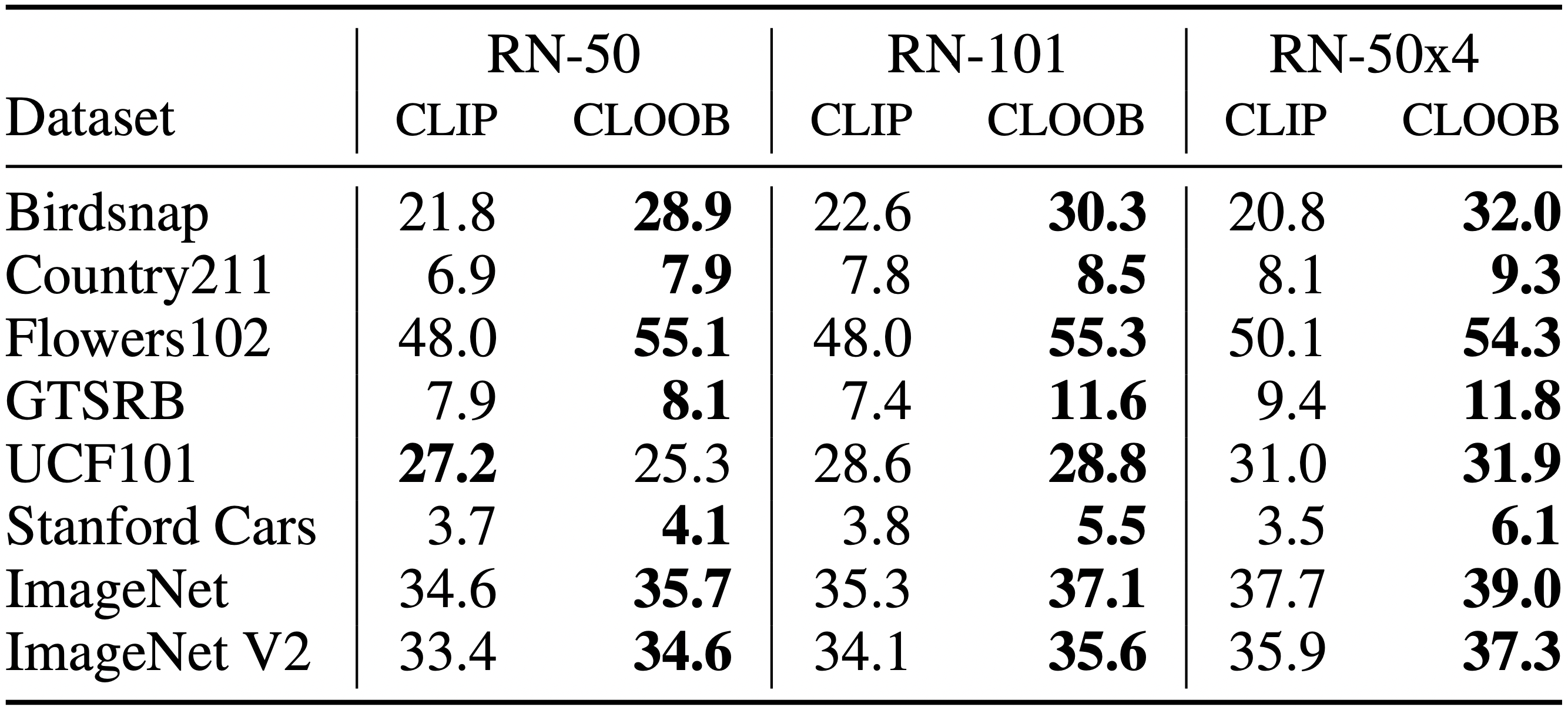
Pretraining Dataset. The YFCC dataset, a subset of YFCC100M (Thomee et al., 2016), has 15 million image-text pairs but the textual description is less rich than for CC and often lacks meaningful information.
Results for Different Encoder Sizes. Zero-shot results for the reimplementation of CLIP and CLOOB using different ResNet architectures trained on YFCC. Using ResNet-50 encoders, CLOOB outperforms the CLIP in 7 out of 8 tasks. The performance of CLOOB scales with increased encoder size.
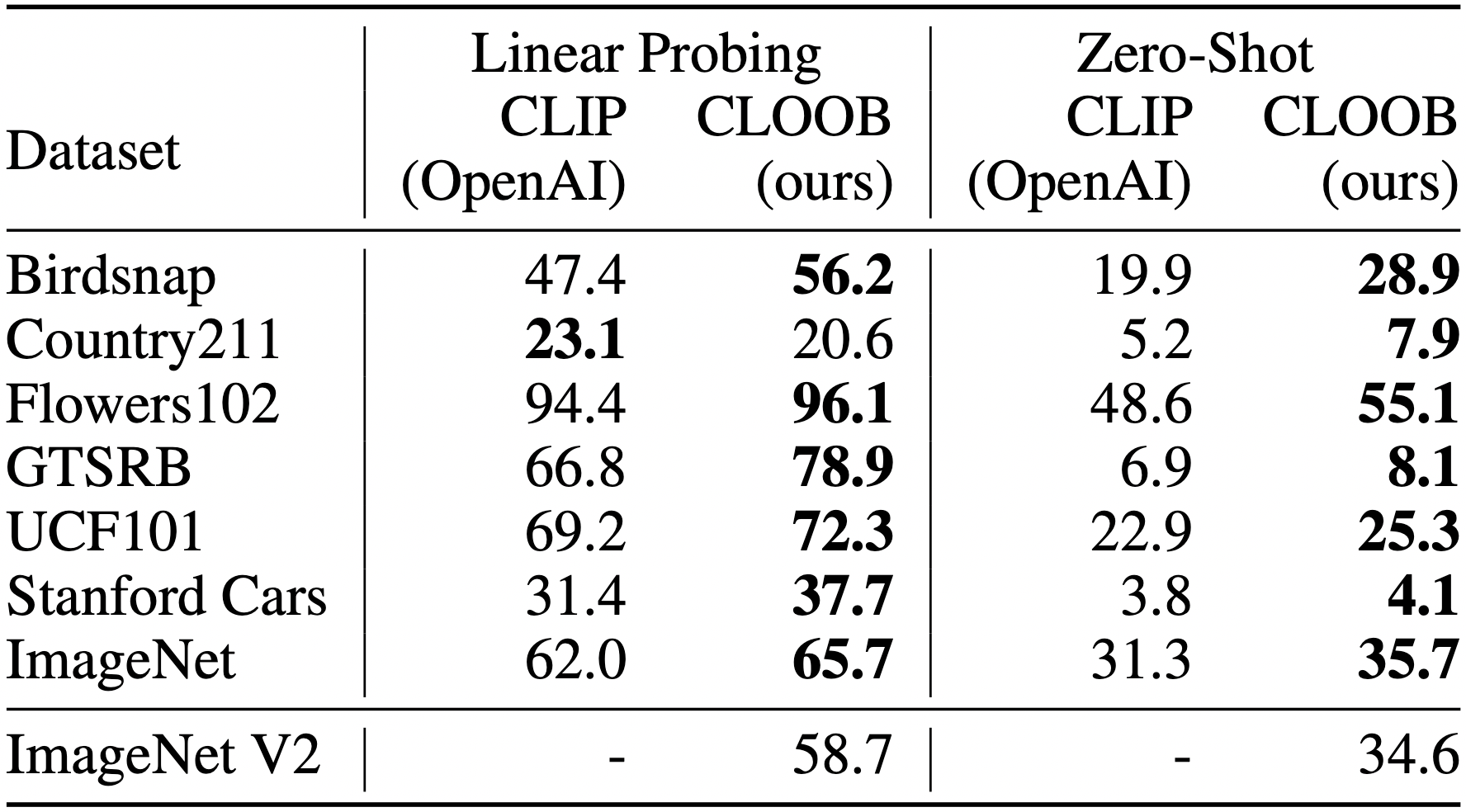
Results Comparing CLOOB to OpenAI CLIP. CLOOB and CLIP trained with ResNet-50 encoder. CLOOB consistently outperforms CLIP across all different downstream tasks for zero-shot.
Code and Paper
Additional Material
-
Paper: Modern Hopfield Networks and Attention for Immune Repertoire Classification
-
Paper: Contrastive learning of image- and structure-based representations in drug discovery
-
Blog post on Energy-Based Perspective on Attention Mechanisms in Transformers
For more information visit our homepage https://ml-jku.github.io/.
Correspondence
This blog post was written by Elisabeth Rumetshofer and Andreas Fürst.
Contributions by Angela Bitto-Nemling, Michael Kopp, Johannes Lehner, Viet Tran, Günter Klambauer and Sepp Hochreiter.
Please contact us via cloob[at]ml.jku.at