[Code] [Paper] [Talk] [Tutorial] [Codebase Demo Video] [BibTeX]

Universal Physics Transformers (UPTs) are a novel learning paradigm to efficiently train large-scale neural operators for a wide range of spatio-temporal problems - both for Lagrangian and Eulerian discretization schemes.

The current landscape of neural operators mainly focuses on small-scale problems using models that do not scale well to large-scale 3D settings. UPTs compress the (potentially) high-dimensional input into a compressed latent space with makes them very scalable. Starting with 32K inputs (scale 1), we scale the number of input points and evaluate the memory required to train such a model with batchsize 1. In this qualitative scaling study, UPTs can scale up to 4.2M inputs (scale 128), 64x more than a GNN could handle.

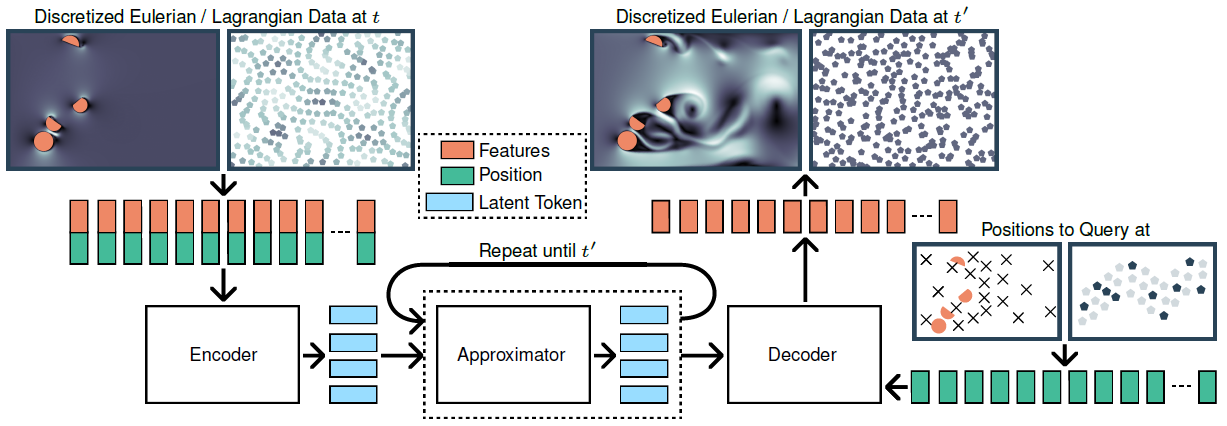
The architecture of UPT consists of an encoder, an approximator and a decoder. The encoder is responsible to encode the physics domain into a latent representation, the approximator propagates the latent representation forward in time and the decoder transforms the latent representation back to the physics domain.

To enforce the responsibilities of each component, inverse encoding and decoding tasks are added.

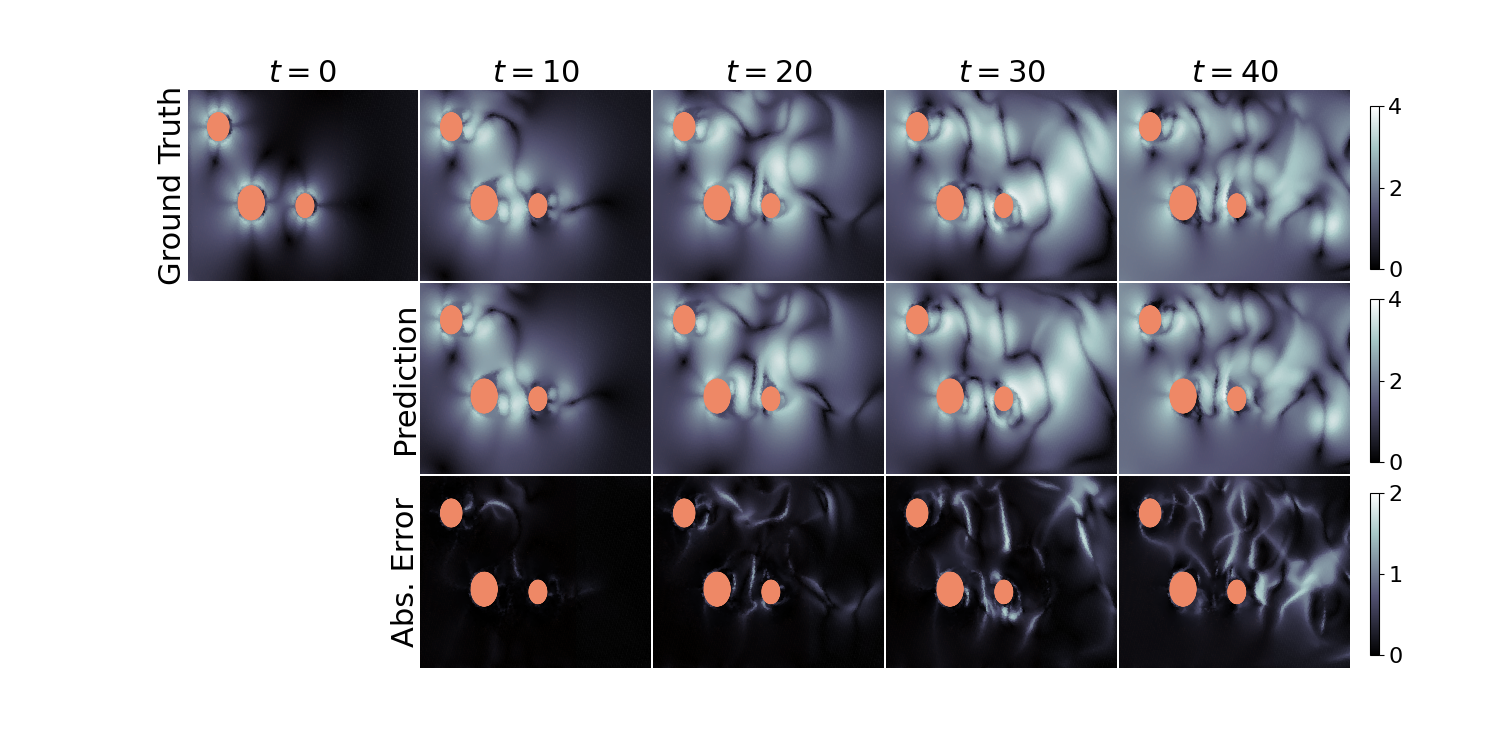
UPTs can model transient flow simulations (Eulerian discretization scheme) as indicated by test loss and rollout performance (measured via correlation time):

UPTs can also model the flow-field of particle based simulations (Lagrangian discretization scheme):

Particles show the ground truth velocities of particles and the white arrows show the learned velocity field of a UPT model evaluated on the positions of a regular grid.